Manacher's Algorithm

What is ‘palindromic string’?

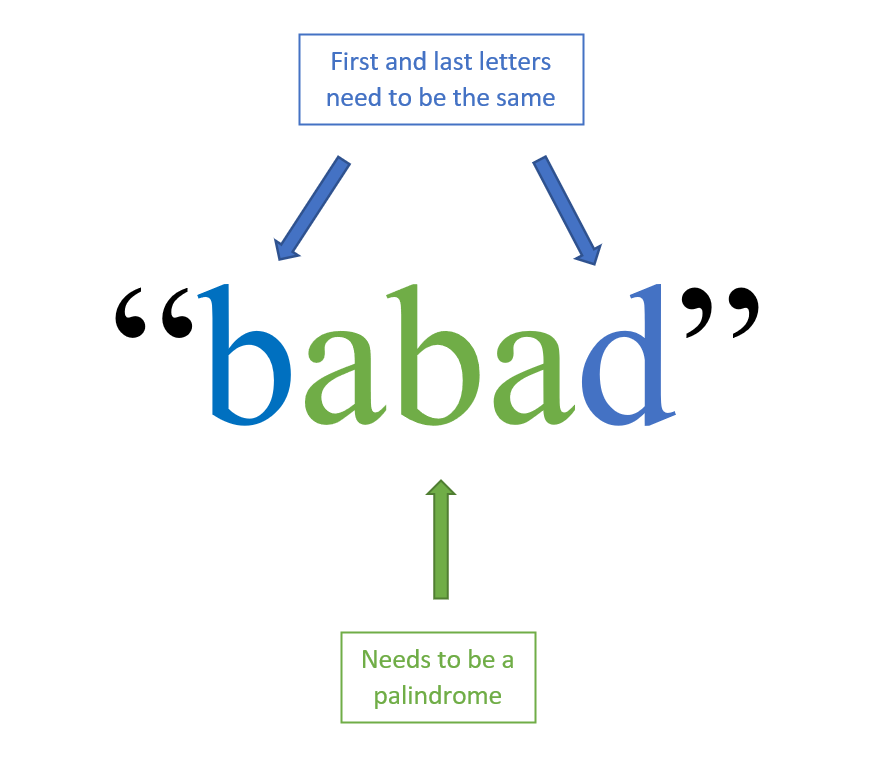
A string is what is a palindrome if the string read from left to right is equal to the string read from right to left.

Brute Force

Brute force solution will find Palindromic Substring.

1. Find all Substring.
2. Check if it is Palindromic or not. It has O(1) space complexity. But, it has \(O(n^3)\) time complexity. It seems to need less time complexity.

Expand Around Center

We could solve it in \(O(n^2)\) time complexity using only constant space.

1. Fix a center. Every character can be a center.
2. Calculate how long palindromic substring can be made with the center.
3. Need to check not only [center-i:center+i] but also [center-i:center+i+1]. Be ready for case ‘abba’.

Manacher’s Algorithm

Manacher’s Algorithm is most powerful to find Palindromic Substring in a string. It has \(O(n)\) time complexity. It reduces time complexity by using previous results. Let’s see how it works.

1. Manacher’s algorithm can’t find palindrome with even-characters. So, we need to insert ‘#’ or some characters to find it. For example, ‘banana’ should be transformed ‘b#a#n#a#n#a’.
2. \(index\) will change from 0 to \(N\)(string length) and calculate how long(A) can make palindrome with \(index\).
3. Check if \(index\) that is calculating could be part of palindrome which alread made before. When \(j\) change from 0 to \(index\), \(r = max(j+A[j])\). \(p\) is \(j\) which makes maximum \(r\).
4. (case \(index>r\)) If not, \(A[index]\) need to initialize 0. Because previous results can’t help calculating how long(A) can make palindrome with \(index\). \(A[index]=0\)
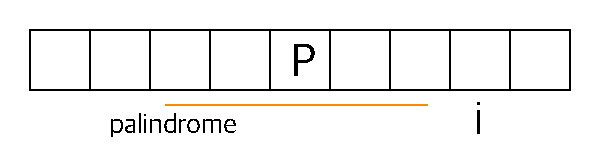
5. (case \(index<=r\))In opposite case, we can use previous results. Find \(index\)’s symmetry point with \(p\). \(A[index]=A[2p-index]\)
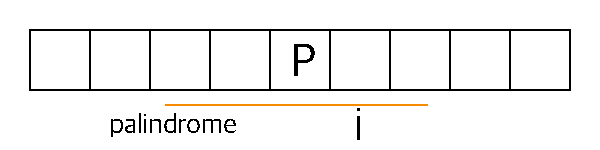
6. After initializing \(A[index]\), increase \(A[index]\) while \(S[index-A[index]]=S[index+A[index]]\). Half of palindrome’s charaters don’t need to calculate by using symmetry point’s result. It is the reason why time complexity reduces.

class Solution:
    def longestPalindrome(self, s: str) -> str:
        #step1
        T = '#'.join(f'#{s}#')
        n = len(T)
        A = [0] * n
        r = p = 0
        #step2
        for i in range(1, n - 1):
        #step4,5
            A[i] = (r > i) and min(r - i, A[2 * p - i]) 
        #step6
            while i - 1 - A[i] >= 0 and i + 1 + A[i] < n and \
                    T[i + 1 + A[i]] == T[i - 1 - A[i]]:
                A[i] += 1
        #step3
            if i + A[i] > r:
                p, r = i, i + A[i]
        maxLen, centerIndex = max((n, i) for i, n in enumerate(A))
        return s[(centerIndex - maxLen) // 2: (centerIndex + maxLen) // 2]